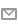Analýza funkce pro výpočet koeficientu Rlog
Když se na mne na poslední seriálové soutěži Seriálu MIČR v září 2024 v Jinolicích obrátila Lenka s dotazem na možné limity koeficientu Rlog, vzpomněl jsem si na první semestr matematiky na technice, na průběh exponenciální funkce a nic zlého netuše odpověděl, že nejspíše žádné limity nejsou. Nicméně jsem slíbil, že se na průběh funkce Rlog = f(R) podívám a pokusím se matematicky nalézt její extrémy.
Trochu mne zamrazilo v zádech, neboť ke stanovení extrémů funkce je třeba provést první derivaci funkce podle R a tuto položit rovnu nule. Pravda, během mé praxe v projekční kanceláři jsem derivování použil několikrát po absolvování školy, kdy na nás, mladé inženýry, starší spolupracovníci zkoušeli různé „špeky“. Od té doby zřídka. K překonání této překážky jsem požádal o pomoc studentku MF UK, vítězku matematických olympiád, která extrémy hravě vyřešila během několika málo minut. Kromě toho jsme řešili i inverzní body funkce kdy druhá derivace se rovná nule. Tyto body však nemají pro naši praxi význam. Dále nebudu podrobně rozepisovat postup řešení derivace, uvedu pouze výsledné vzorce pro extrémní hodnoty. Pro názornost jsem průběh funkce zobrazil v grafu.
Výchozí stav
Jako výchozí podklad jsem použil část platných pravidel NAVIGA, ods. 13.3.3, kde je uveden vztah ke stanovení Rlog:
kde:
Lwl = délka (plně vystrojeného) modelu na vodorysce [mm],
S = plocha plachet [m2],
V = výtlak [kg],
K = 456.
Konstanta K = 456 je stanovena:
aby při Lwl = 456 [mm], S = 1 [m2] a V = 1[kg], nabyl parametr R hodnotu R = 1.
Parametr R je funkce 3 proměnných; jejich kombinace může být nekonečná.
Dosadíme-li za R = 1 do vztahu pro Rlog obdržíme také Rlog = 1.
V bodě R = 1 se nachází první inflexní bod.
V dalším kroku stanovíme parametr Rlog=f(R) kde:
pro R≥1 platí:
pro R <1 platí:
Stanovení extrémů funkce R_log =f(R):
K matematickému stanovení extrémů funkce byly využity dovednosti studentky MF UK, která dokázala derivovat (na rozdíl ode mě) výše uvedenou funkci podle R a za použití metod matematické analýzy stanovit její maxima a minima.
Minimum funkce:
pro
Maximum funkce:
pro
Obecně platí: pro R=0 je hodnota R_log= +∞
pro R= +∞ je hodnota R_log=0
Grafické znázornění funkce
Pro představu průběhu funkce jsem provedl zobrazení v programu EXCEL – viz obr. níže.
Pro grafické znázornění je třeba vytvořit tabulku dat hodnot R, stanovit Rlog a vhodným typem grafu zobrazit závislost obou hodnot (v připojeném pdf ke stažení).
Na vodorovnou osu (x) jsou vyneseny hodnoty R, na svislou osu (y) vypočtené hodnoty Rlog.
Hodnoty R jsou stanoveny za předpokladu proměnné Lwl v intervalu Lwl= <80,2500>[mm]. Hodnoty S=1 a V=1 jsou konstantní v celém intervalu.
Závěr
Z grafického průběhu funkce je patrno, že pro naši praxi má smysl pro stavbu modelu využít oblast nacházející se mezi výše uvedeným minimem a maximem funkce. Nejvyšší přírůstek Rlog je patrný v okolí R = 1. Čím více se blíží hodnota R k extrémním bodům, klesá gradient (přírůstek) Rlog.
K posouzení využití reálné oblasti grafu v praxi jsem použil startovní listinu EC NAVIGA 2017 (známá Kristýna) kde bylo zúčastněno 49 modelů. Interval R zúčastněných modelů se nacházel mezi hodnotami <0,475, 1,417>. Z grafu je vidno, že pro R = 0,475 se nacházíme před minimem funkce (červená svislá čára) a hodnota Rlog je vyšší než by byla v minimu. V oblasti maximálních R je určitá rezerva (zelená svislá čára).
Využití znalosti průběhu funkce Rlog = f(R) dává staviteli možnost optimalizace dílčích parametrů modelu třídy NSS
Zpracoval: Ing. Ladislav Hanuška
Datum: 31. 12. 2024
Diskutujte
Děkuji Borkovi za připojení cenných poznámek z praxe.
Souhlasím s tím, že Rlog je pouze fyzikální koeficient vycházející ze základních parametrů modelu a sám o sobě neznamená, že je zárukou vysoké výkonnosti. Důležité je, že díky němu je možné v jednotlivých třídách porovnat výkony modelů s různými parametry.
Laďa
Láďova analýza je provedena s pro něj typickou pragmatickou precizností, a je bezezbytku správná. Doplňuji pouze, že konstanta 456 byla před více než 30 lety zavedena proto, aby referenční loď (Rubin od firmy Graupner) nabyla v původním lineárním vzorci hodnotu 1,00. Zároveň se tím dosáhlo adaptace „Universal Rule“ z roku 1903, která byla předlohou lineárního vzorce, na modelové podmínky. Viz.
https://en.wikipedia.org/wiki/Universal_rule
Avšak i Láďova definice je správná, poněvadž se jedna o tutéž matematickou funkci. Moje poznámka má tedy pouze hodnotu historické anekdoty.
Přestože je původní otázka Láďovou analýzou zodpovězena, je možné z grafického znázornění vyčíst řadu dalších velmi zajímavých věci. Především dramatický zlom průběhu funkce v oblasti Rlog=0,75 napovídá, že vzorec cíleně znevýhodňuje příliš malé modely. Toto bylo hlavním cílem zlogaritmovani v roce 1997/8. Zabránilo to (praxí ověřeným) siruacim, kdy model, který projel cílem jako poslední s odstupem přes 20 minut, vyhrával přepočtem přes směšné malý handicap.
Nabízí se otázka, která oblast průběhu funkce je s ohledem na úspěšnost v závodě nejvýhodnější. Moje vlastní zkušenosti se dvěma rozdílnými modely („Sýkorka” Rlog=0,75 a “Marie” Rlog=0,87) říkají, že je možné systematicky vyhrávat s oběma, pokud se ovšem podaří přizpůsobit styl jízdy jejich specifickým vlastnostem. Rozdíl je pouze v tom, že vyhrát s větším modelem je těžší a zábavnější, s menším modelem pak snazší ale nudnější.
Můj německý kamarád Erwin Doerzapf tvrdí, že optimální hodnota Rlog
leží mezi 0,81 a 0,83. Zdůvodňuje to tím, že se jedna o nejvýhodnější kompromis mezi ještě pořád nízkým handicapem a již solidním výkonem modelu. Tato teorie je nejspíš správná, avšak - jak už Láda psal - interakce tři proměnných ve vzorci nabízí nekonečné množství kombinaci, a tím i různých konstrukčních řešení. Navíc vyjadřuje handicap pouze fyzikální teoretický POTENCIÁL modelu, nikoliv jeho skutečnou VÝKONNOST. O vlivu počasí, schopnostech skipera a v NSS vlivu statického hodnocení ani nemluvě.
Proto univerzálně platné optimum zřejmě neexistuje, což mě osobně těší, protože to dělá celou záležitost zajímavější.
S pozdravem
Borek Dvořák
Zajímavé...
Děkuji Láďovi že tomu věnoval čas a energii. Vypočtené výsledky jsou opravdu zajímavé a díky tabulce je o čem přemýšlet....
Moc děkuji Láďovi (a jeho týmu) za zpracování skvělé analýzy k diskutovanému tématu, které vzniklo takhle jednou v podvečer na soutěži pod stanem.
Po mnoha letech se tak do Teorie přidal další článek - rok 2025 začínáme hezky zostra.
Mám už fotky z jedné loděnice, čekám na doprovodný text a těším se na další příspěvky od Vás, kamarádi...
Do nového roku přeji úspěchy v modelářské dílně (loděnici) a také na soutěžích v sezóně 2025! Kalendář je základně naplněn - informace budou průběžně doplňovány.
Jirka
| Po | Út | St | Čt | Pá | So | Ne |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Akcí: 17
Uživatelů: 130
Lodí v registru: 3
08.11. 50. Fuehlinger See Regatta
01.11. Těrlicko 2025
22.10. Pinczow 2025
28.09. Duchcov 2025 od Ladouse

 čtvrtek
18.
prosinec 2025
čtvrtek
18.
prosinec 2025
 RSS
RSS Mapa stránek
Mapa stránek Přihlásit se
Přihlásit se